Cum funcţionează Legea lui Arhimede? Mecanica clasică

Arhimede a înţeles cu mai bine de 2200 de ani în urmă principiul care în prezent îi poartă numele, şi anume faptul că un corp cufundat într-un fluid este împins de jos în sus cu o forţă egală cu greutatea volumului de fluid dezlocuit de acesta. Cum oare, altfel decît pe cale experimentală, se poate demonstra această lege? 

Arhimede şi naşterea expresiei celebre - "Evrika!"

Mulţi dintre noi cunosc povestea momentului de mare inspiraţie al lui Arhimede care a născut celebra expresie "Evrika!" (ro. "am găsit !"). Marele savant grec al antichităţii a rostit binecunoscuta exclamaţie - spune legenda - cînd, intrînd în cada de baie şi observînd că nivelul apei a crescut, a înţeles că volumul de apă dezlocuit trebuie să fie egal cu volumul unei părţi a corpului său, cea aflată în apă.

Ceea ce înseamnă că Arhimede tocmai descoperise o modalitate de calcul foarte precisă pentru volumul corpurilor de forme neregulate, o problemă ce părea de nerezolvat la acea vreme. Legenda spune că emoţia pe care i-a produs-o revelaţia sa a fost aşa de puternică, încît Arhimede ar fi ieşit imediat din baie direct pe străzile Siracuzei, gol-puşcă, pentru a le comunica tuturor descoperirea.

Cine a fost Arhimede?

Arhimede a trăit între anii 287-212 î.Hr. în oraşul Siracuza, în Sicilia, care la vremea respectivă era colonie grecească. Este unul dintre cei mai cunoscuţi învăţaţi ai Greciei antice, matematician, fizician, inginer, inventator şi astronom, privit ca fiind cel mai mare matematician al antichităţii şi unul dintre cei mai mari ai tuturor timpurilor. Este cel care a pus bazele hidrostaticii şi a explicat principiul pîrghiei.

Legea lui Arhimede

Arhimede mai este cunoscut şi datorită celebrului principiu care îi poartă numele şi care ne învaţă că "un corp cufundat într-un fluid este împins de jos în sus cu o forţă egală cu greutatea volumului de fluid dezlocuit de acesta". Legea se aplică atît în cazul lichidelor, cît şi al gazelor, iar dacă enunţul anterior pare prea tehnic, cîteva exemple din viaţa de zi cu zi vor face în mod cert lumină.

Acest principiu este cel care stă la baza faptului că ne simţim mai uşori în apă ori a faptului că la momentul ieşirii la suprafaţa apei dintr-o fîntînă găleata "devine" brusc mai grea. Mai mult, tot folosind legea lui Arhimede se poate explica şi de ce nave de mare tonaj se menţin la suprafaţa apei mărilor şi oceanelor ori de ce baloanele umplute cu heliu se ridică în atmosfera terestră.

Verificarea pe cale experimentală a legii lui Arhimede

Legea poate fi verificată în mod practic extrem de simplu, cu ajutorul unui cîntar cu arc, a unui recipient cilindric umplut pe jumătate cu apă şi a unei pietre, astfel: se măsoară iniţial greutatea pietrei şi se notează nivelul apei în cilindrul gradat. Ulterior, piatra atîrnată de acul cîntarului este introdusă în apă. Indicaţia instrumentului de măsurat se modifică, asemenea nivelului apei din recipient. Un calcul simplu, care are la bază valoarea cunoscută a densităţii apei, egală cu 1 gram/cm³, ne arată că volumul de lichid dezlocuit de piatră cîntăreşte exact cît diferenţa dintre valorile indicate la început, respectiv la final, de către cîntar.

Ansamblu folosit pentru verificarea
pe cale experimentală a legii lui Arhimede

O demonstraţie teoretică simplificată a principiului

Se pare deci că Arhimede a intuit ce se întîmplă, în urmă cu aproximativ 2200 de ani, fiind primul om despre care se ştie că a înţeles fenomenul ce-i poartă în prezent numele. Ce nu cunoaşte prea multă lume este în ce mod, altfel decît prin efectuarea unor măsurători, se poate demonstra acest principiu al fizicii cunoscut încă din antichitate. O demonstraţie riguroasă necesită fundamente teoretice, iar nu simple măsurători.

O variantă simplificată de demonstraţie teoretică a legii lui Arhimede

Pentru a demonstra principiul, vom considera un caz particular. Vom folosi o piesă metalică (ori dintr-un material de densitate mai mică) paralelipipedică pe care o vom agăţa de arcul cîntarului şi apoi o vom cufunda într-un recipient umplut parţial cu lichid, asemenea pietrei din figura anterioară. La momentul în care piesa metalică atinge o stare de echilibru, asupra sa acţionează următoarele forţe:

G - greutatea sa,

T - o forţă ascensională determinată de tensiunea din arcul cîntarului,

cît şi forţele datorate presiunii exercitate de lichid pe suprafeţele piesei metalice (F₁şi F₂).

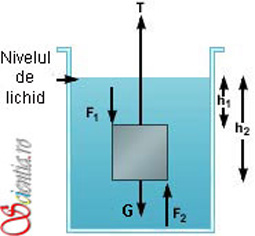
Presiunea provocată de lichid acţionează, conform legilor cunoscute ale fluidelor, din toate direcţiile şi are valoare proporţională cu adîncimea. Mai mult, presiunea se defineşte ca forţă/unitate de suprafaţă, iar presiunea în interiorul unui fluid, într-un anumit punct, este proporţională cu înălţimea (adîncimea) la care punctul este situat în raport cu suprafaţa (marginea de sus) lichidului, multiplicată cu densitatea fluidului - ρ şi cu constanta gravitaţională - g.

Conform principiilor mecanicii newtoniene, ajungem la următoarele relaţii matematice pentru un corp aflat în echilibru de mişcare:

T+F₂=G+F₁.

F₁=P₁*S = h₁*ρ*g*S, unde P₁ reprezintă presiunea hidrostatică exercitată pe suprafaţa superioară a piesei, iar S este suprafaţa feţei superioare, egală ca valoare cu cea a feţei inferioare a paralelipipedului,
F₂=P₂*S = h₂*ρ*g*S, unde P₂reprezintă presiunea hidrostatică exercitată pe suprafaţa inferioară a piesei.

Din cele trei relaţii de mai sus rezultă că pierderea de greutate a piesei metalice introduse în lichid şi anume G-T=(h₂-h₁)*ρ*g*S=ρ*g*(Volumul piesei)=(Masa volumului de lichid dezlocuit)*g= Greutatea volumului de lichid dezlocuit (q.e.d.).

Forţa arhimedică reprezintă rezultanta tuturor forţelor (de apăsare) cu care lichidul, datorită presiunii hidrostatice, acţionează asupra unui corp scufundat în acesta. În cazul de faţă, unul ideal, ales astfel pentru uşurinţa demonstraţiei, forţa rezultantă pe feţele laterale ale piesei metalice este nulă deoarece acţiunea lichidului pe feţele opuse este aceeaşi, ducînd la anularea reciprocă a acestor componente ale presiunii hidrostatice. În cazuri apropiate de cele reale, calculul rezultantei acestor forţe de apăsare datorate presiunii hidrostatice necesită cunoştinţe matematice avansate.

Scris de Scientia.ro